Once upon a time, I came across an interesting little math puzzle game called Everest. The rest of this post is going to have spoilers, because even talking about the game inevitably gives away the nature of the puzzle that is at its core, so before reading I highly urge you to go check it out for yourself — there’s an online version (though it sadly doesn’t save your progress) if you don’t want to or can’t download Android apps.
Done that? Or just don’t care?
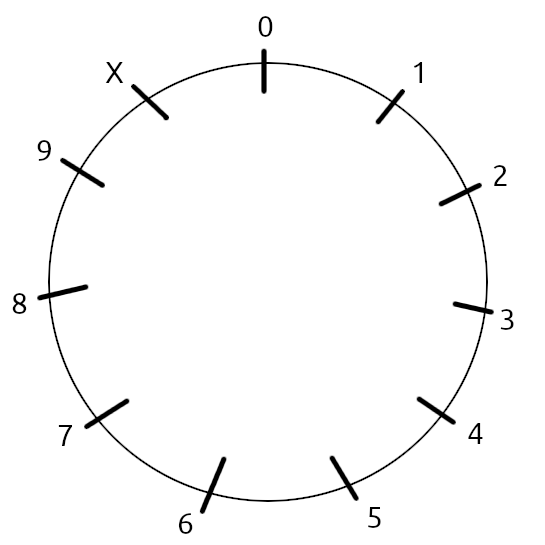
The gimmick behind Everest is that it operates in base 11 modular arithmetic. Like a clock face, except with 11 places instead of 12, and each number has only one digit; 10 is represented as X, and 11 is the same as 0. 0 minus 1 is X, so X is negative one. Adding 9 is the same as subtracting 2.
Anyway, I reached level 10 or 11 doing just mental math, but it was slow and frustrating. Then I realized I could use pencil and paper to help me so I jotted some things down and eventually came up with a couple tools:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | X |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 6 | 8 | X | 1 | 3 | 5 | 7 | 9 |
| 3 | 6 | 9 | 1 | 4 | 7 | X | 2 | 5 | 8 |
| 4 | 8 | 1 | 5 | 9 | 2 | 6 | X | 3 | 7 |
| 5 | X | 4 | 9 | 3 | 8 | 2 | 7 | 1 | 6 |
| 6 | 1 | 7 | 2 | 8 | 3 | 9 | 4 | X | 5 |
| 7 | 3 | X | 6 | 2 | 9 | 5 | 1 | 8 | 4 |
| 8 | 5 | 2 | X | 7 | 5 | 1 | 9 | 6 | 3 |
| 9 | 7 | 5 | 3 | 1 | X | 8 | 6 | 4 | 2 |
| X | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
I can’t figure out a way to geometrically represent the rule added in level 7, but there are a few easy things to keep in mind:
(in particular, )
I mean, it’s pretty obvious what’s going on algebraically. I just wish there was some kind of chart I could draw to make it easier at a glance.